November 2020
Improving computational methods for imaging Earth's interior
Seismology offers the most powerful tool for characterizing the subsurface structure of Earth. Earthquakes occurring near the surface and as deep as 700 km emit elastic waves that are recorded by seismometers on Earth's surface. The shapes and arrival times of the recorded waves can be compared with seismograms modeled in a relatively simple, starting description of Earth's inner structure. By quantifying seismogram differences, seismologists can formally improve the description of Earth's structure by performing an inverse problem known as tomography. Tomography, best known in the medical fields, is about characterizing variations in a 3D medium (human body, oil reservoir, Earth's mantle) without directly measuring the properties.
Over the past 20 years, advances in computational methods and high-performance computing have enabled a new, more accurate form of seismic tomography. Previously the tomographic problem began with a simple description of Earth, whereby analytical methods could be used to represent wave propagation and measurement sensitivities. Now, it is possible to begin with a more accurate and complex 3D description of Earth, while also using 3D numerical simulations to account for realistic complexities of wave propagation.
On paper, seismic tomography is a straightforward optimization problem: define a misfit function based on seismogram differences, determine how to calculate the gradient of the misfit function, and then minimize the misfit function. However, in practice, the problem is challenging for three reasons: a) the Earth is extremely heterogeneous, making it difficult to characterize in a numerical description, b) the optimization workflow of tracking thousands of seismic wavefield simulations and millions of seismograms is cumbersome, and c) with millions of unknown model parameters, it is challenging to quantify uncertainties in the estimated model.
In a recent contribution, Bryant Chow and colleagues [Chow et al., 2020] unveil an improved procedure for performing seismic tomography with wavefield simulations [Fig. 1]. Chow established a software package pyatoa (https://github.com/bch0w/pyatoa) linking several existing tools together, including SPECFEM3D, for performing synthetic and real seismic tomographic inversions on a high-performance computing environment. The workflow includes data retrieval, wavefield simulations, time window selection for measurements, calculation of adjoint sources, adjoint wavefield simulations, and iterative optimization. These procedures run on an HPC cluster without user intervention, thereby accelerating the science while also promoting reproducibility. They demonstrate the method in the North Island of New Zealand, where seismic station coverage enables imaging the crustal structure at length scales of tens of km horizontally and a few km vertically [See Fig. 2]. The new software should lower the barrier for new users interested in performing state-of-the-art seismic imaging.
Contributed by:
Carl Tape
University of Alaska Fairbanks
References
Chow, B., Kaneko, Y., Tape, C., Modrak, R., and J. Townend. (2020). An automated workflow for adjoint tomography—waveform misfits and synthetic inversions for the North Island, New Zealand. Geophysical Journal International, 223, 1461–1480, https://doi.org/10.1093/gji/ggaa381
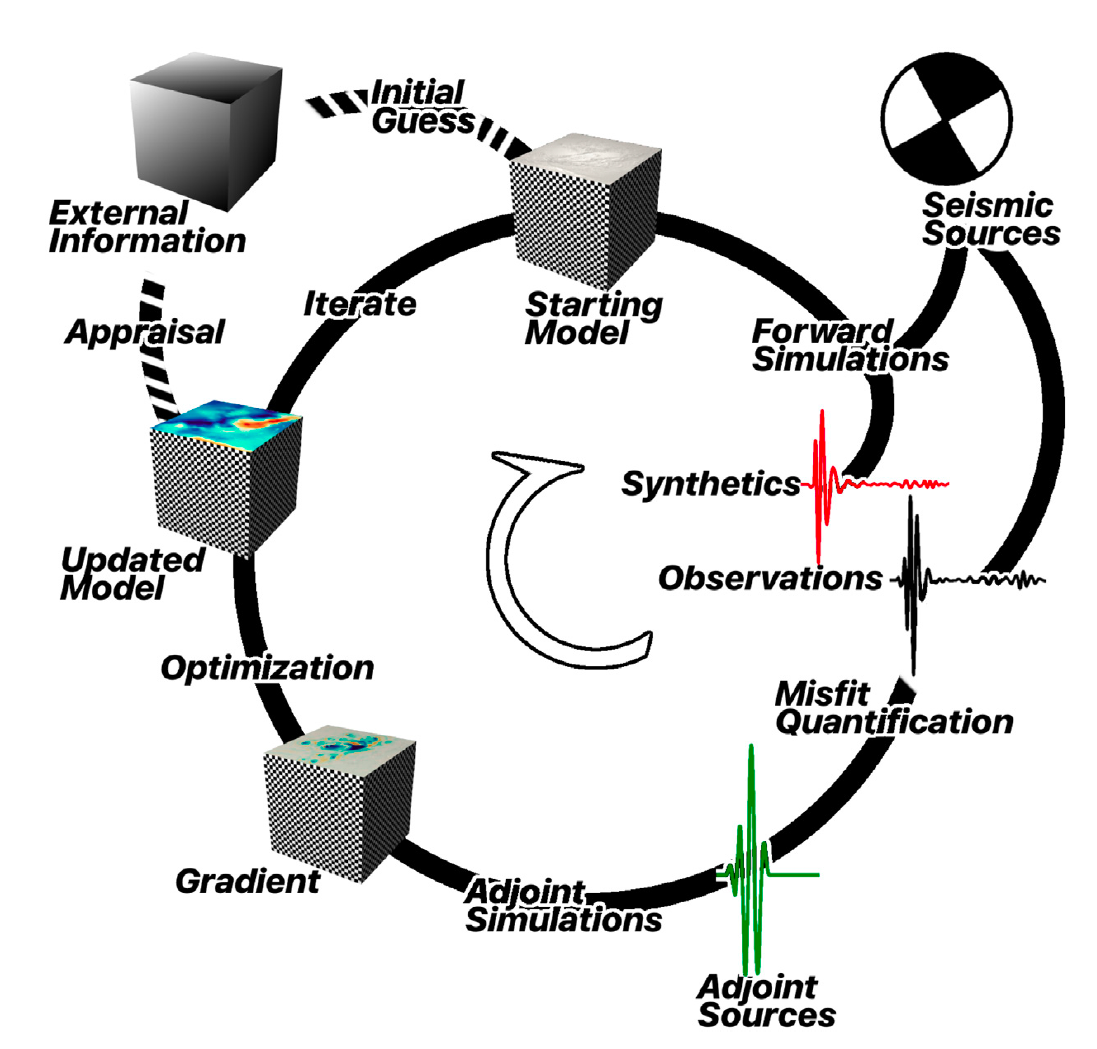
Figure 1. A diagrammatic illustration of the adjoint tomography workflow. The workflow tools introduced in this paper are capable of automating all components of the adjoint tomography workflow, except for the initial guess, creation of the starting model and the appraisal of the final model using external information. Inversions can be run fully-automated, or with various levels of manual intervention introduced throughout the inversion.

Figure 2. Finite-element mesh used for wavefield simulations in the North Island of New Zealand. Element sizes increase with depth, since higher velocities allow for larger elements while maintaining comparable numerical accuracy. This mesh was used for synthetic and real tomographic inversions.
