Code Scaling
- Details
- Published on Sunday, 08 November 2020 07:30
Code scaling performed on XSEDE, ACCESS or Frontera resources for select CIG community codes.
ASPECT
Strong-scaling results for ASPECT on the XSEDE cluster Stampede2 Skylake nodes. The scaling is derived from the wall-clock time of a thermal mechanical model run for two time steps.
[jpg]
Calypso
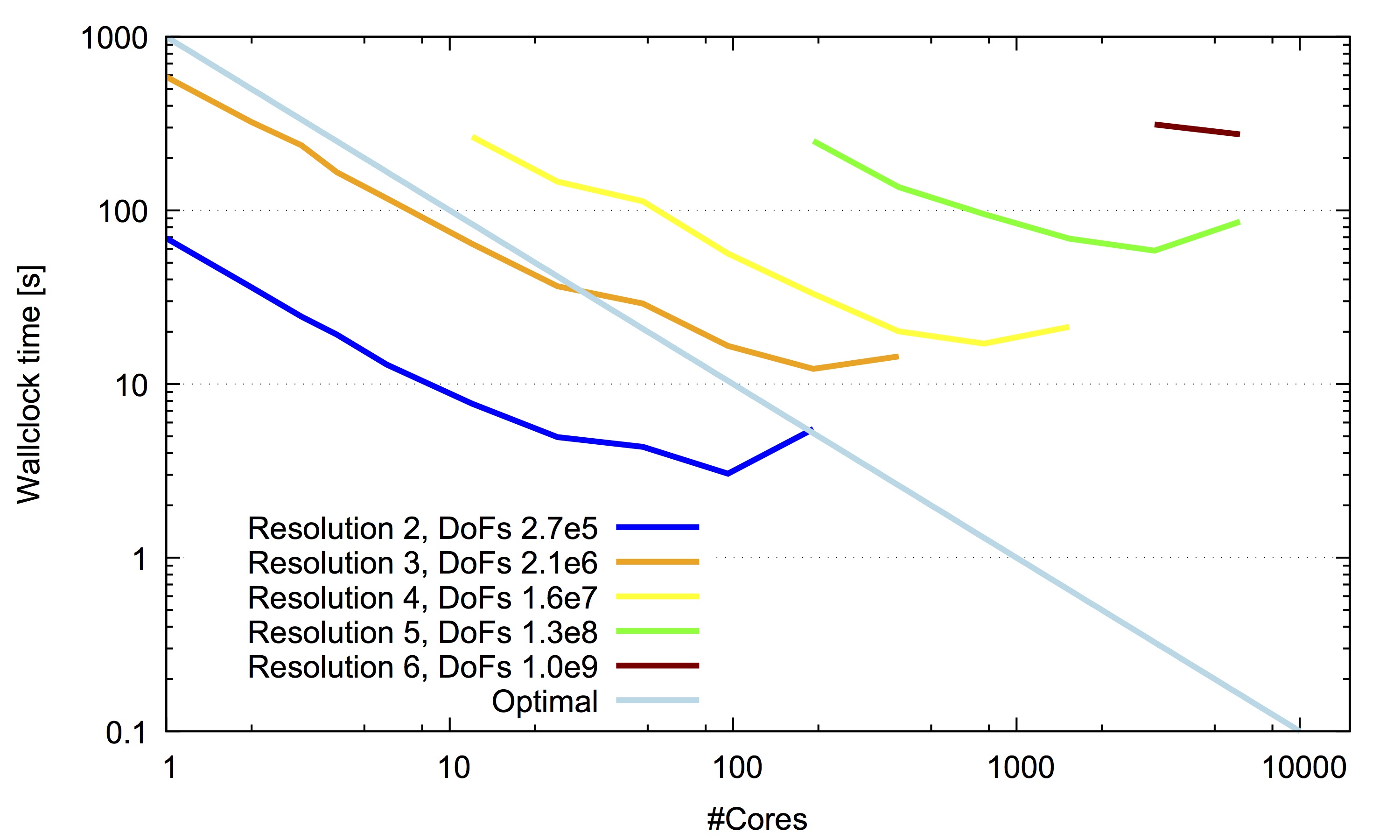
The largest scaling test above corresponds to roughly a 17 million elements and scales well up to 16384 cores.
Comparison of Calypso's scaling on the TACC Stampede and Stampede 2. Strong scaling results is shown in the left panel, and weak scaling results are shown in the right panel. Ideal scaling is plotted by solid lines.
CitcomS
Tests were perfromed on TACC Lonestar for a regional model with 6.4 million unknowns using up to 256 cores.
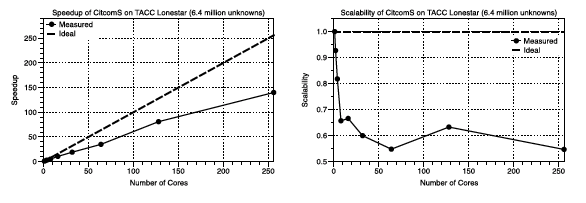
Speedup (left) [pdf] and scalability (right) [pdf] of CitcomS on Lonestar.
Rayleigh
Rayleigh is based on the solar dynamo code ASH which scales efficiently to 10,000 cores. We expect similar performance for Rayleigh.
Rayleigh has been benchmarked on ALCF MIRA using up to 131,072 single-threaded cores for the Geodynamo Working Group benchmarking exercise.
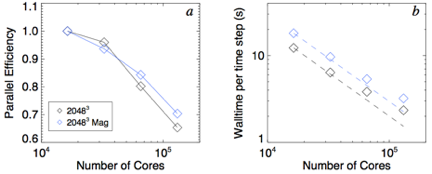
Left: The parallel efficiency for the non-magnetic and magnetic runs at the 20483 problem size. Efficiency is defined as the ratio of the realized speedup to the ideal speed-up. deal performance is taken relative to 16,384 cores, the minimum core count or this problem size. Right: Strong scaling results for the ame set of runs. Ideal scaling for each series is indicated by the dashed line. [png]
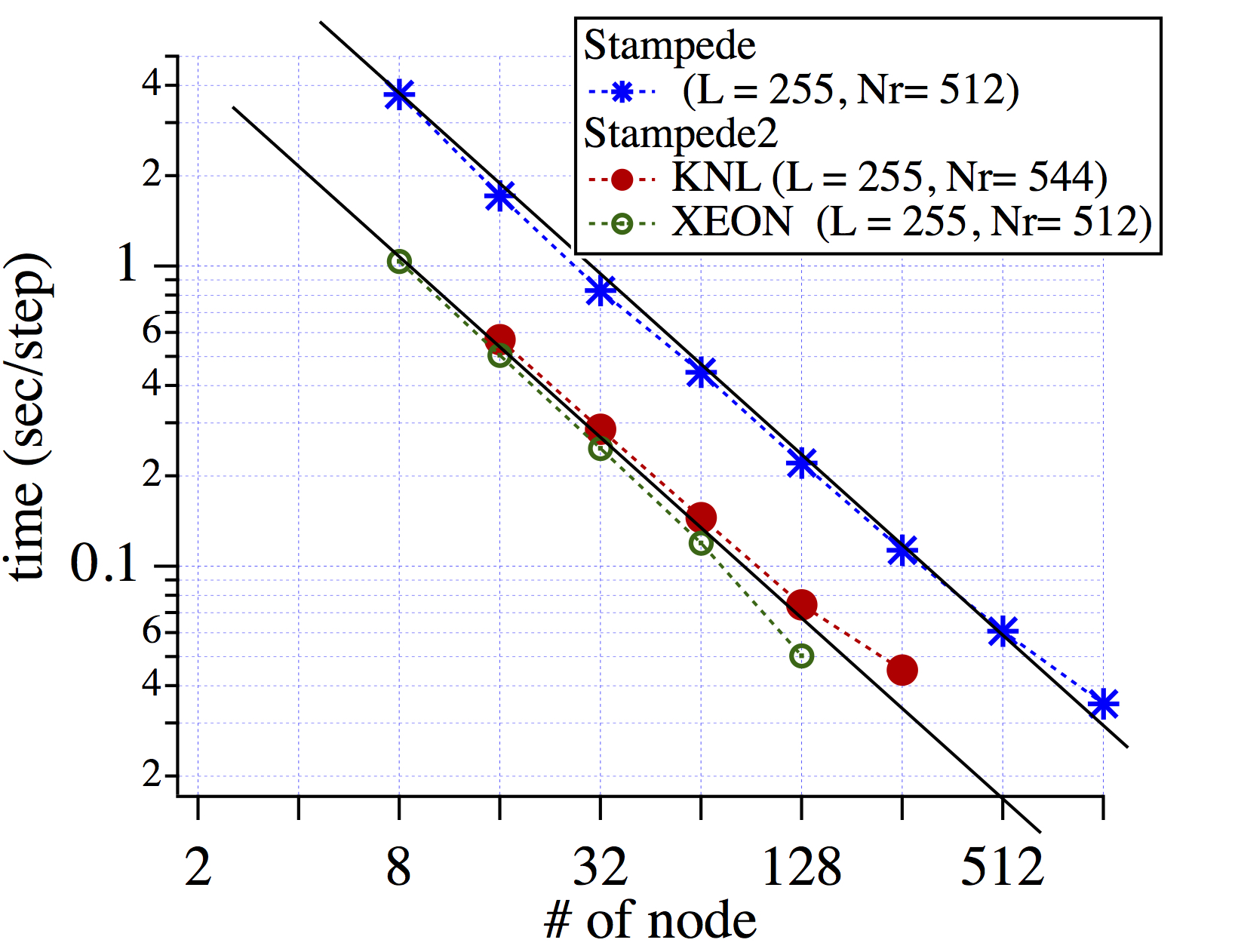
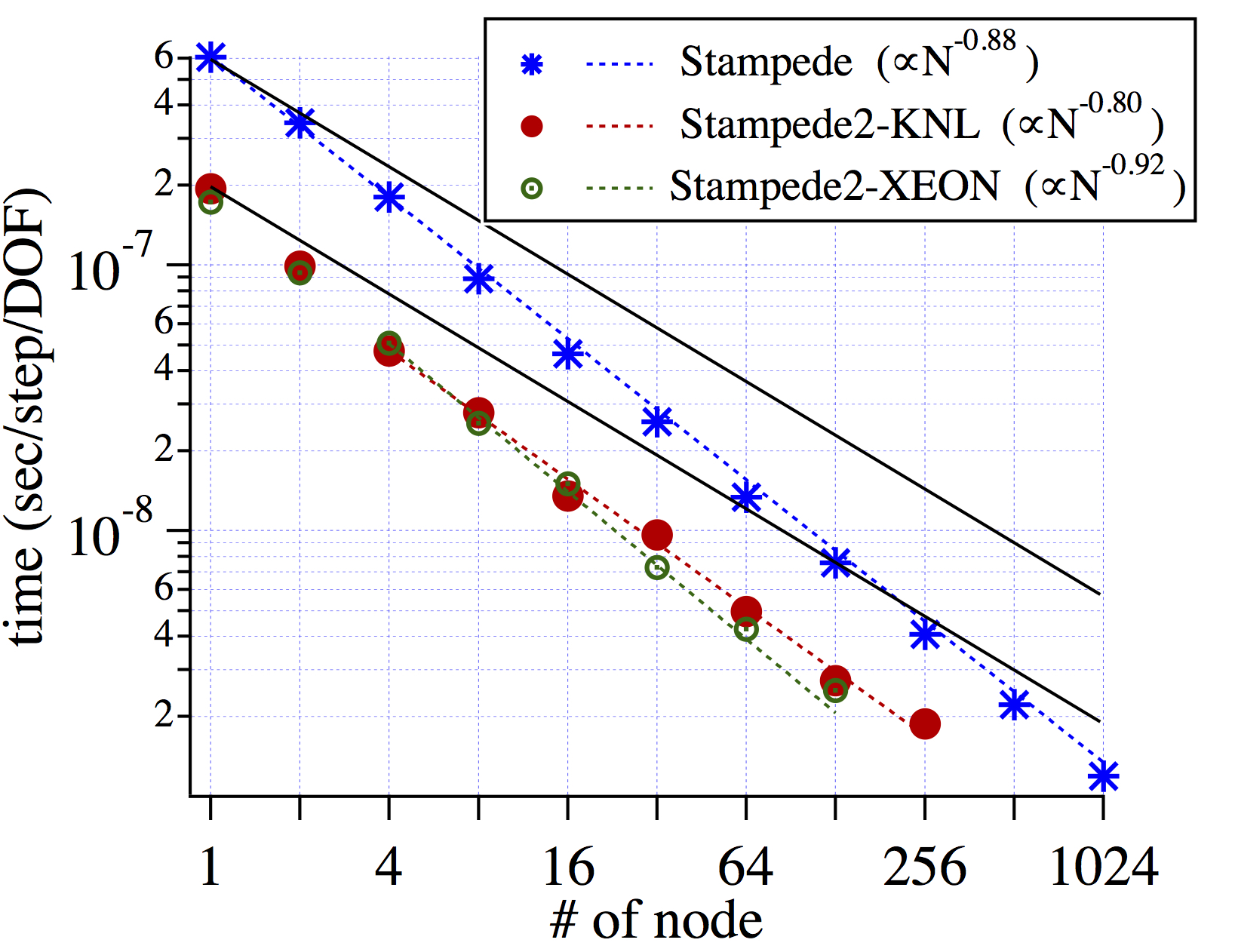
Rayleigh's scaling on the TACC Stampede 2. Strong scaling results are shown in the left panel, and weak scaling results are shown in the right panel. Ideal scaling for the strong and weak scaling, is plotted by solid lines. Rayleigh only uses MPI parallelization, and 64 of 68 processor cores are used in the each KNL node.
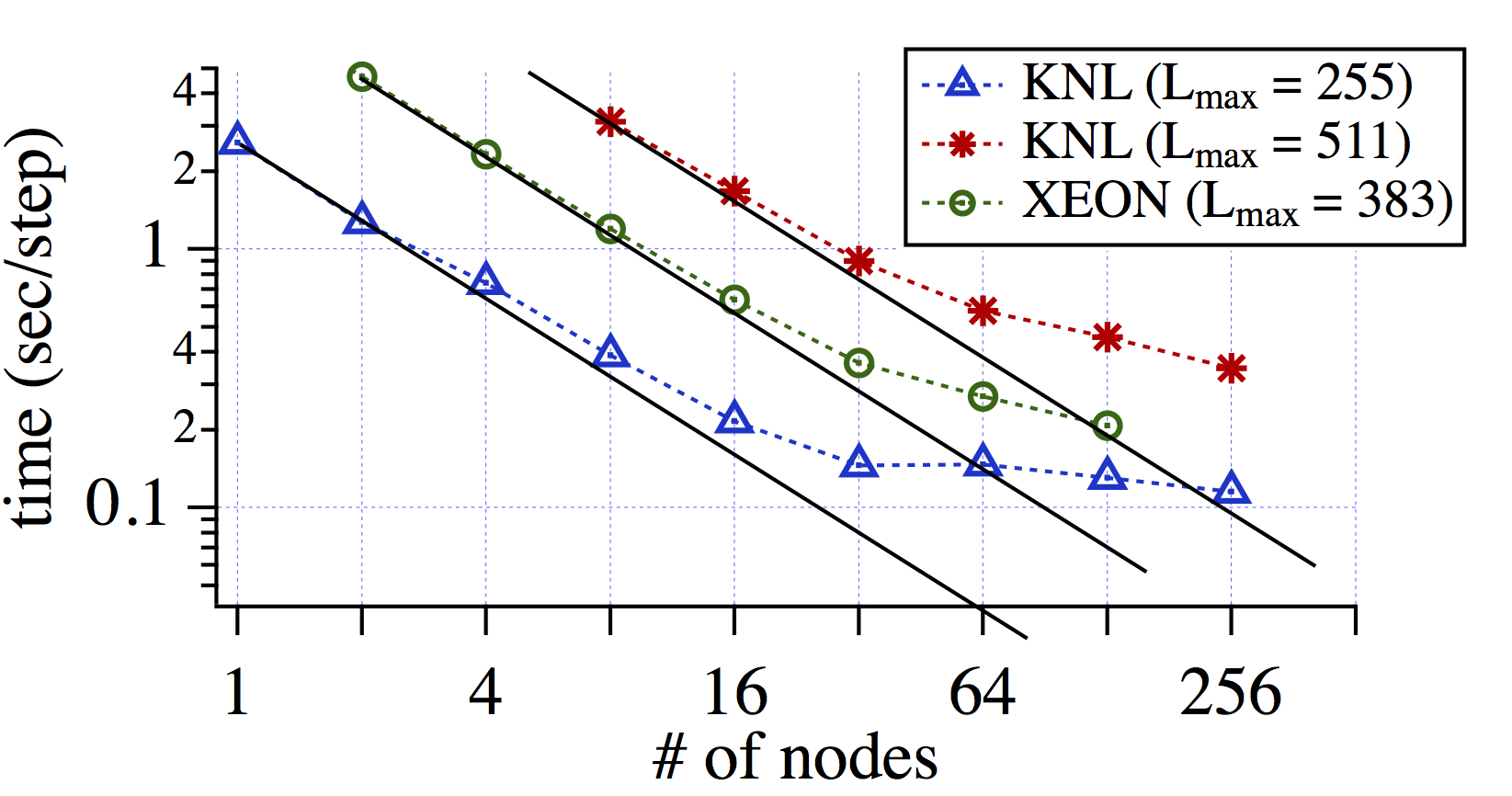 .
. 
SPECFEM3D_GLOBE
SPECFEM3D_GLOBE simulates global and regional (continental-scale) seismic wave propagation using the spectral-element method (SEM). The SEM is a continuous Galerkin technique, which can easily be made discontinuous; it is then close to a particular case of the discontinuous Galerkin technique, with optimized efficiency because of its tensorized basis functions
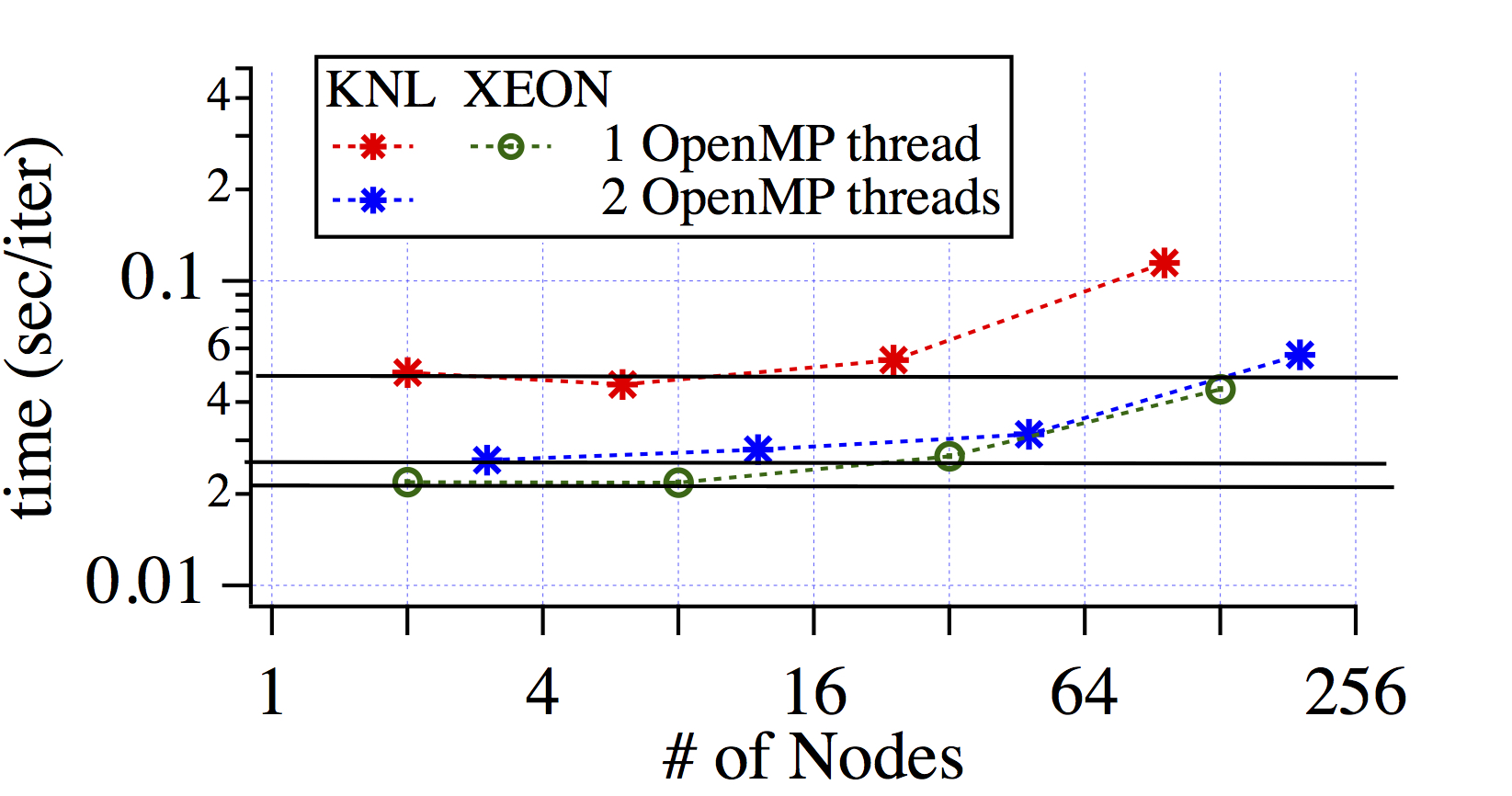
Strong scaling results is shown in the left panel, and weak scaling results are shown in the right panel. Ideal scaling and constant for the strong is plotted by solid lines. In the scaling tests for the KNL nodes, 64 of 68 processor cores are used and 1 or 2 OpenMP threads cases are tested.
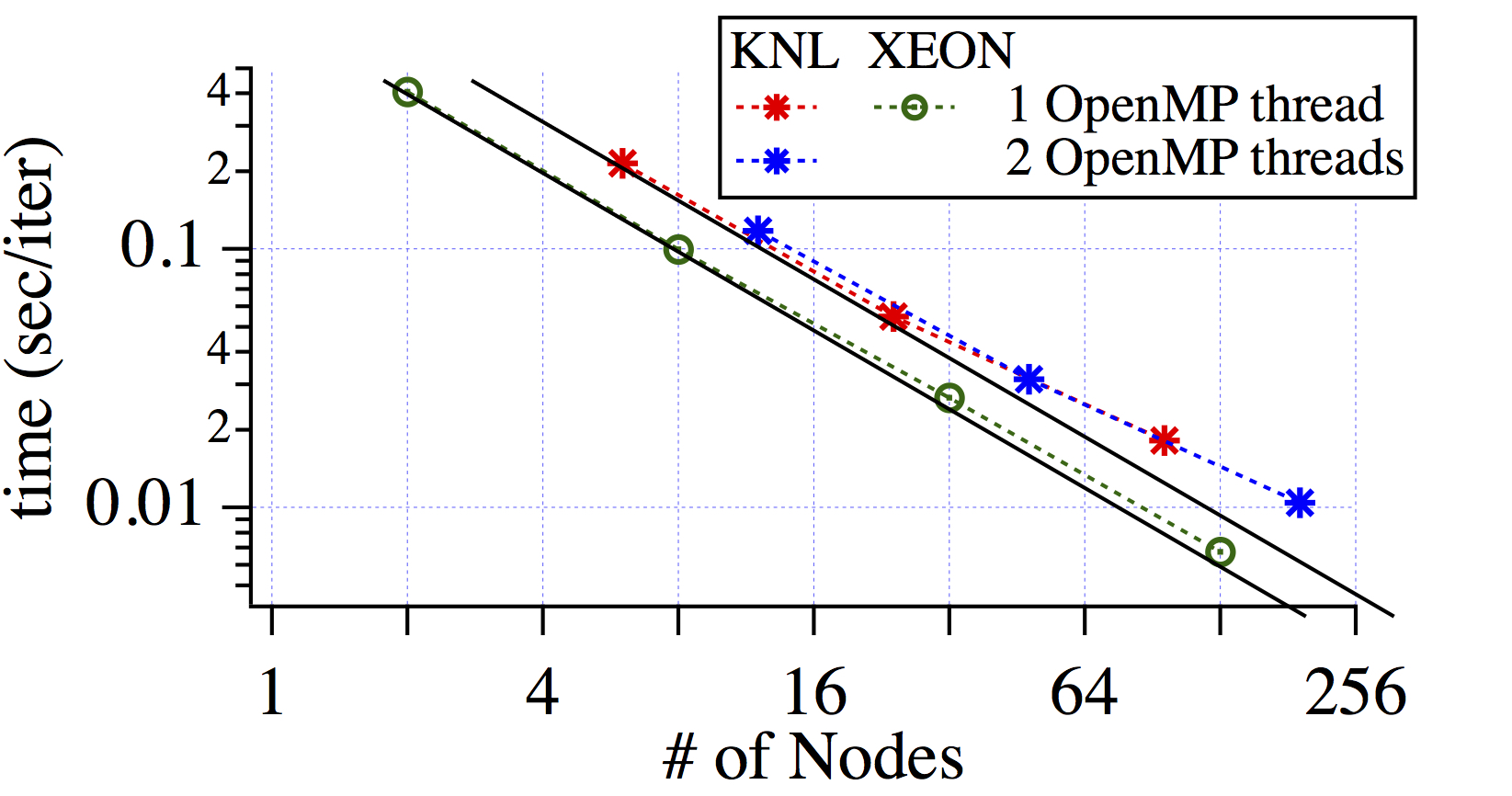 .
.