November 2022
- Details
- Parent Category: resources
- Published on Saturday, 04 September 2021 03:29
SPH Models of the Moon-Forming Giant Impact
The conventional theory for the origin of the Earth’s Moon is the giant impact hypothesis, which describes an oblique, low-velocity collision between the Earth and a Mars-sized planet, Theia (Canup & Asphaug, 2001). Within this framework, the Moon accretes from a debris disk that is produced by the impact. This model can reproduce the mass, dynamics, and low iron content of the Moon. A well-known weakness of the canonical giant impact hypothesis is that the remnants of Theia’s mantle dominate the disk, which contradicts the strong isotopic similarities between the Earth and Moon that suggest a common material origin if the Theia’s isotopic composition differed from the Earth.
Smoothed Particle Hydrodynamics (SPH) is the numerical method of choice for simulating high-energy astrophysical events such as the giant impact. SPH is a particle method in which the typical conservation laws are convoluted onto a proximity-weighted “kernel” function, such that nearby particles have a disproportionately greater influence on a given particle than farther-away particles. SPH therefore decomposes Earth and Theia into a system of interacting particles and can directly simulate the giant impact and the proceeding tens of hours of disk evolution (Figure 1).
Rapidly increasing computational power and the ability to increase simulation resolutions by a few orders of magnitude has recently brought SPH giant impact results under scrutiny, as simulations of different particle resolutions do not always converge on the same results (e.g., Hosono et al., 2017, Kegerreis et al., 2022). In our study, we investigate nonconvergence as it relates to the hardcoded “cutoff density” in SPH. Cutoff densities are typically set in SPH as the minimum density that any particle is allowed to achieve so that unphysical densities are not present in the simulation. Densities in SPH are calculated according to the proximity of other nearby particles in the simulation. In most use cases of SPH, because particles generally remain near one another, the cutoff density is not an issue (such as inside a planet). However, in canonical giant impact simulations, the resulting disk is very low in particle resolution, composing less than 2% of all particles in the simulation. Such a sparse disk means that disk particle densities can fall arbitrarily low and attain the value of the cutoff density, thereby changing the bulk density of the disk and affecting its dynamic and thermodynamic evolution.
We find that very low values of cutoff density (~5 kg/m3) result in disks that are artificially shocked for the duration of the simulation as the distantly spaced disk particles momentarily enter each other’s kernel envelope and produce small, instantaneous density jumps, which leads to higher disk temperatures, entropies, and vapor mass fractions (VMFs) (Figure 2). This phenomenon is not observed at higher values of cutoff density ≥ 500 kg/m3, as the density jumps remain below these cutoff densities. However, cutoff density values that are too high (2000 kg/m3) can suppress vapor production and potentially favor the development of large clumps of particles. We therefore recommend an intermediate cutoff density value of ~500 kg/m3 as a starting point for future SPH simulations.
SPH also requires an equation of state (EoS) to calculate the thermodynamics of the simulation and the amount of vapor in the disk. M-ANEOS (Melosh, 2007) has been a ubiquitous choice of EoS for over a decade owing to its self-consistent ability to capture complex behavior of silicates over a wide range of temperatures and pressures. Because the original M-ANEOS used a Dulong-Petit limit to resolve material heat capacities, it underestimated the heat capacity of liquid forsterite. Recently, Stewart (2020) introduced a new version of M-ANEOS, which we refer to as “Stewart M-ANEOS”, that allows for a user-fitted value to correct material heat capacity. We find that Stewart M-ANEOS produces more massive disks that are less vaporized than the previous version of M-ANEOS (“N-SPH M-ANEOS”).
An EoS that can accurately constrain the vapor fraction of the disk is a first step to modelling the observed depletion of moderately volatile elements (MVEs) in the Moon and the enrichment of heavy MVE isotopes. The heavy MVE enrichment is likely the result of extensive vaporization of the protolunar materials (Nie and Dauphas, 2019). Our future work will use the results gathered from this study to model the propensity of heavy MVE fractionation and the devolatilization of the protolunar material as a function of the disks’ vapor fraction.
The paper associated with this research, “Effect of Heat Capacity and Low Resolution Disks in SPH Models of the Moon-Forming Giant Impact” is currently under review.
Contributed by:
Scott Hull and Miki Nakajima, University of Rochester
References
Canup, Robin M., and Erik Asphaug. "Origin of the Moon in a giant impact near the end of the Earth's formation." Nature 412.6848 (2001): 708-712.
Hosono, Natsuki, et al. "Unconvergence of very-large-scale giant impact simulations." Publications of the Astronomical Society of Japan 69.2 (2017): 26.
Kegerreis, Jacob A., et al. "Immediate Origin of the Moon as a Post-impact Satellite." The Astrophysical Journal Letters 937.2 (2022): L40.
Melosh, H. J. "A hydrocode equation of state for SiO2." Meteoritics & Planetary Science 42.12 (2007): 2079-2098.
Nie, Nicole X., and Nicolas Dauphas. "Vapor Drainage in the Protolunar Disk as the Cause for the Depletion in Volatile Elements of the Moon." The Astrophysical Journal Letters 884.2 (2019): L48.
Stewart, Sarah T., et al. "The shock physics of giant impacts: Key requirements for the equations of state." AIP conference proceedings. Vol. 2272. No. 1. AIP Publishing LLC, 2020.
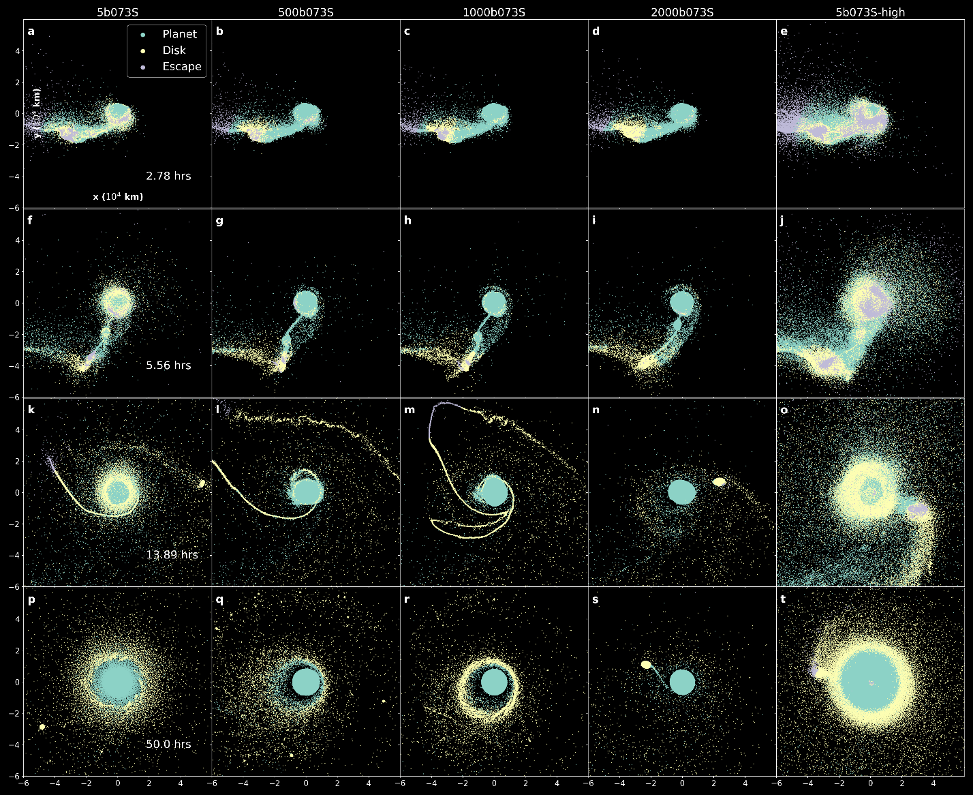
Figure 1. Evolution of SPH simulations of the canonical giant impact with varying values of cutoff density using Stewart M-ANEOS (see main text for details). The first four columns from left-to-right represent increasing values of cutoff density: 5, 500, 1000, and 2000 kg/m3 using 1.1 million particles. The right-most column uses a cutoff density of 5 kg/m3 and 10.1 million particles. Each row represents a different time snapshot of the simulation. Each particle is color-coded based on whether it is part of the Earth (green), disk (yellow), or escaping the system (purple).

Figure 2. Time evolution of the disk for simulations of varying cutoff density. (a). Average disk entropy, (b). Average disk temperature, (c). disk vapor mass fraction, (d). disk mass, (e). disk angular momentum, (f). disk mass fraction sourced from Theia. The blue line shows a cutoff density of 5 kg/m3 and the associated artificial shocks.
