Milestone 2: Results and Analysis
Details the results of the Milestone 2 simulations and analyzes the accuracy of the advection scheme.
Model descriptions
The second milestone contains several different models. In each a porosity distribution has been supplied, which acts as a force term on the stokes equation. The porosity is advected according to a semi Lagrangian scheme, with no natural diffusion. Details of these models are given below.
Simple Gaussian porosity field
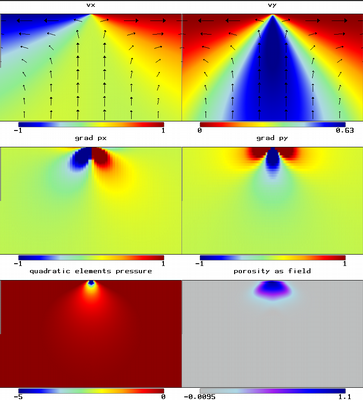
The first model is a simple demonstration of how the porosity dependent force term drives the porosity distribution up through the domain. The domain is subjected to free slip boundary conditions, which also distort the porosity distribution as it is advected. This model is housed in the directory:
Magma/Models/Milestone2/ZPNM_SemiLagrangianPorosity/
with the XML file to be passed at run time being the Porridge.xml file.
Gaussian Porosity Field Advection. Advection of Gaussian porosity field as a Stokes equation force term. The lower density porosity region rises due to gravity.
Ridge model with Gaussian porosity distribution
The second model is an extension of the first milestone, that is a ridge model with the initial boundary conditions loaded from a reference solution. However in this case a Gaussian porosity distribution has been added. The porosity distribution is distorted as it moves up through the domain in accordance with the velocity field generated from the boundary conditions. This model can be found in:
Magma/Models/Milestone2/RidgeModelWithGaussianPorosity/
with the XML file to be passed being Ridge2D.xml.
Ridge Model with Gaussian Porosity Field. Stokes flow with 2D ridge model boundary conditions and Gaussian porosity initial distribution, driven by a porosity dependent force term.
Validation of the advection scheme
As well as the models, a test is also supplied for validating the accuracy of the semi Lagrangian advection scheme. This involves an initial porosity distribution (either Gaussian or a diagonal line step function, as determined from the XML), which is subjected to a static shearing velocity field. The porosity distribution is subjected to the velocity field for a finite number of time steps (as determined from the XML input file), before the velocity field is reversed and the distribution advected back for the same number of time steps. The normalised global L2 error between the initial and final distributions is then calculated. This test is housed in the directory:
Magma/Models/Milestone2/tests/
And may be run using the input file testSemiLagrangianAdvection.xml.
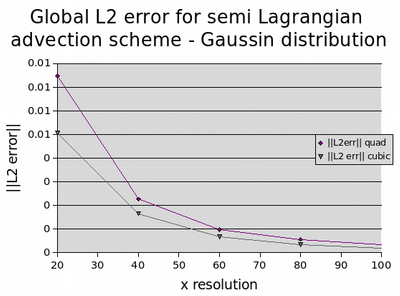
Running this simulation at varying resolutions, the convergence of the errors for the advection scheme were determined using both the Gaussian distribution and diagonal step function as initial conditions. The errors were recorded for schemes which used a cubic method as well as a quadratic method based on the element shape functions for interpolating the value at the end point of the characteristic. As can be observed from the convergence errors plots below, the quadratic and cubic interpolation method schemes converged at comparable (less than linear) rates using the step function initial condition, with an improvement in those results obtained using the cubic interpolation method. When the Gaussian initial distribution was applied (which was easier to solve accurately on account of the smoother gradients involved), both interpolation methods converged at a rate much better than linear, with the cubic interpolation method proving far superior to the quadratic method.
Semi Lagrangian Advection Scheme Test
 |
 |
| Step Function. Diagonal step function initial distribution subjected to a shearing velocity field. | Gaussian Distribution. Gaussian initial distribution subjected to a shearing velocity field. |
Error Convergence for Advection Scheme
 |
 |
| Step Function IC. Normalised global L2 errors for semi Lagrangian advection scheme with a diagonal step function initial condition as a function of resolution. | Gaussian IC. Normalised global L2 errors for semi Lagrangian advection scheme with Gaussian initial distribution as a function of resolution. |