August 2023
- Details
- Parent Category: resources
- Published on Sunday, 22 August 2021 23:29
Revisiting Open Source Libraries for Solving ODEs
Research highlight
Many of CIG’s large flagship codes – for example Rayleigh, PyLith, SPECFEM, and ASPECT – solve partial differential equations. There is of course a long history of writing such codes, and part of this history is that traditionally, PDE solvers have hand-rolled their own time integrators and nonlinear solvers: Exceptions – such as PyLith – notwithstanding, they generally use low-order time discretization methods (such as explicit or implicit Euler, Crank-Nicolson, or BDF-2) with time-step sizes based on CFL numbers rather than accuracy considerations; and they implement nonlinear solvers via fixed point iterations or relatively simple variations of Newton’s method, but without sophisticated line search, trust region, or acceleration methods.
This reliance on hand-written methods is perhaps surprising because we have all learned that at least for the discretization of PDEs, we should build on one of the widely used software libraries that provide everything one needs for the task: Meshes, descriptions of meshes, sparse linear algebra, parallelization to 1000s of MPI processes. It is even more surprising considering that well-written and well-documented ODE solver libraries predate PDE libraries by at least one, perhaps two decades. One could speculate about reasons, but the matter of fact is that PDE solvers generally do not use high-order methods with adaptive time step control based on estimates of the accuracy obtained as part of the solution process (for example in the way the popular Runge-Kutta 45 scheme uses embedded Runge-Kutta formulas).
Within the ASPECT project, we have decided that it is time to re-think this strategy. ASPECT builds on deal.II, a finite element library that has over the years also grown interfaces to many other software packages such as Trilinos for sparse parallel linear algebra, p4est for parallel meshes, and SUNDIALS, among many others. SUNDIALS – short for SUite of Nonlinear and DIfferential/ALgebraic Equation Solvers – is a software package with roots going back to the VODE variable order differential equations solvers in the 1980s, and whose authors this year received the SIAM/ACM Prize in Computational Science and Engineering. It implements both Runge-Kutta methods in its ARKode sub-package, and multistep methods in its CVODE sub-package (along with a host of other methods). It can choose the time step and the order of the method automatically and adaptively. In order to support implicit solvers, it also has a package to solve nonlinear problems, KINSOL, which can use Newton or fixed point techniques, decide automatically about step lengths and whether or not it is time to re-compute the Jacobian. Most of these are state-of-the-art techniques not currently used in ASPECT, which uses a BDF-2 time stepping scheme with a step length based on the CFL number for the flow simulation, and a Newton scheme with line search and Eisenstat-Walker tolerance for solving the nonlinear Stokes equations.
The deal.II library has spent much effort on its interfaces to nonlinear and ODE solvers in the last couple of years. It will take many years before ASPECT will make use of these interfaces throughout the code base, but as a first step we have decided that for the next release – 3.0, planned for the summer of next year – we will make SUNDIALS a required dependency in the same way as Trilinos and p4est are also already required. As in many large code bases, there are numerous parts that could benefit from building on these interfaces, some requiring more and others less work to convert. One patch by Juliane Dannberg (Unversity of Florida) is already pending: ASPECT uses an operator splitting scheme to compute chemical reactions on every node as a small ODE system (see fig. 1), utilizing fixed time-step explicit Euler method; it took less than 100 lines of code to convert this to use deal.II’s ARKode interfaces. Other places we hope to convert are complicated material models that compute the viscosity from an implicit relationship that requires a Newton-type iteration currently implemented by hand, and that could benefit from KINSOL’s ability to do this more efficiently. A long-term goal is to also convert the nonlinear Stokes solver to KINSOL.
Where all of this will go remains to be seen. What is certain is that building on external packages will lead to more efficient and robust codes in the same way as building CIG’s codes on external discretization libraries has allowed us to write far more capable solvers than would have been possible had we decided to write everything from scratch. Starting with small projects such as the reaction solver or a viscosity model also helps build human resources: People who understand the interfaces to SUNDIALS, who can review patches, and guide others to use these interfaces instead of hand-rolling their own algorithms. All of this seems like a worthwhile goal.
Contributed by: Wolfgang Bangerth, Colorado State University Fort Collins; Juliane Dannberg, University of Florida; Rene Gassmoeller, University of Florida
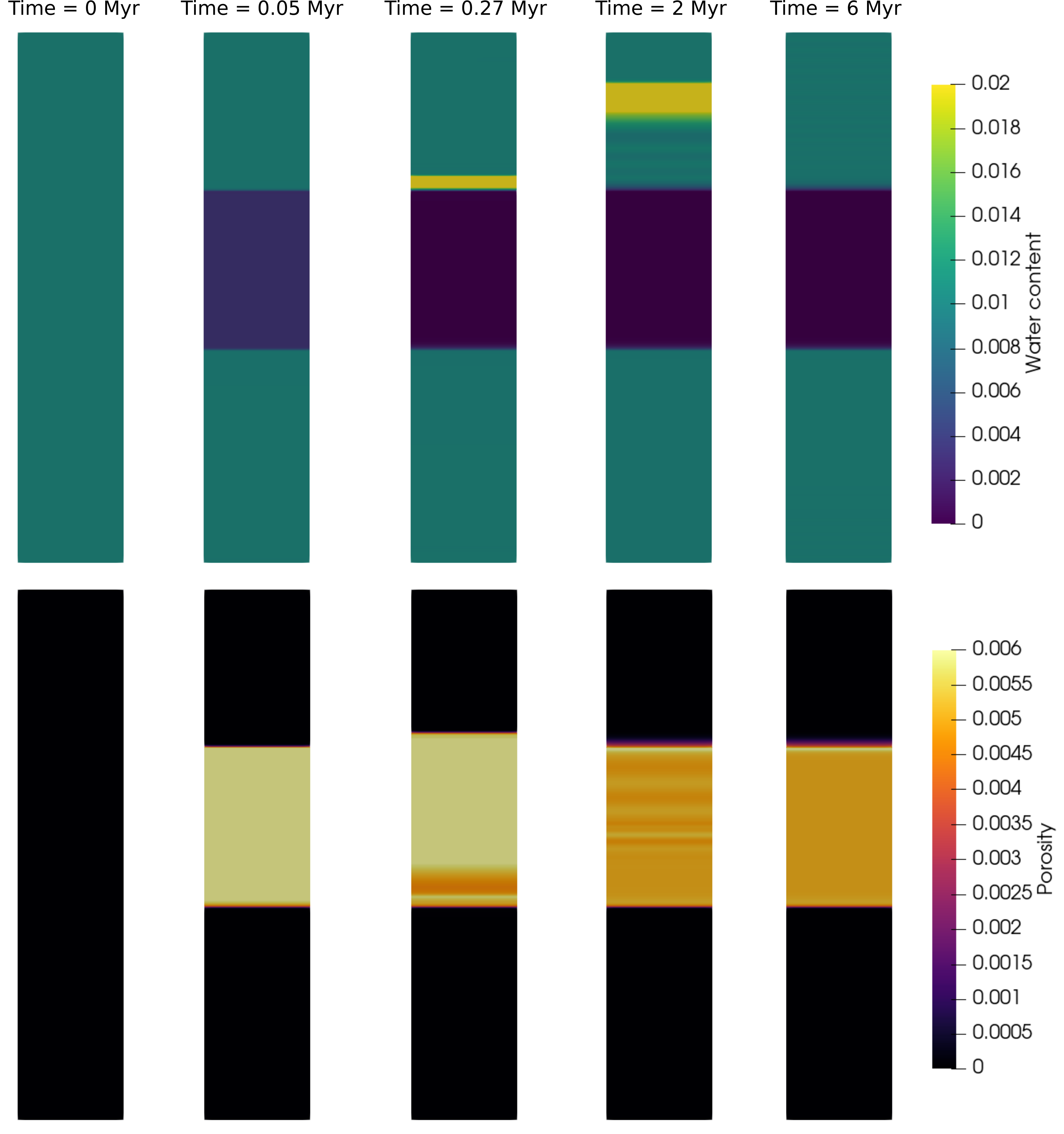
Figure 1. Evolution of the bound water content (top) and the free water (bottom) in a geodynamic one dimensional pipe flow model. Initially, all water is bound (left column). Since the middle layer has a zero solubility, water is almost instantaneously released from minerals and starts migrating upward with respect to the solid, leading to a higher bound water content when it reaches the top layer. Chemical reactions like these are typically much faster than the flow velocity in geodynamic models and are amongst the problems we want to solve by including dedicated ODE solver libraries.
